【下克上】東大生が偏差値40の小学生を1年で御三家に合格させる 第12講【6月】

こんにちは。とある東大生です。
昨日マンスリーテストを終えた直後のところの授業です。
テストを終えて次の日でしたので、若干気が抜けているというか、
テンションが入ってない日だったので今日は1時間で切り上げてきました。
マンスリーといった目先のテストばかりにとらわれるのではなく、来年の2/1から逆算して一喜一憂せずに頑張るのが大事と以前申し上げましたが、たまにはこういった日もあっていいと考えています。
メリハリも大事なので。
ということで、今日はいつものメニューではなく、
頭を使ったちょっとした遊びを用いた授業をしてきました。
それは「御三家の問題を解いてみよう」という企画です。
今回はちょうどいい問題を探していたら灘中の問題があったので
それを解かせてみました。
灘は関西の学校なので、関東の御三家ではありませんが
「灘・甲陽・東大寺」と並ぶ関西の御三家の中のトップランナーなので
ご容赦していただけると幸いです。
遊びの問題の選定基準としては、
「頭を使えば一発で解ける・煩雑な計算を必要としない」
で選んでいるので
整数の問題を選ぶことが多いです。
今回も整数の問題です。
それでは問題を見てみましょう。

【灘の入試問題にチャレンジ!!】
2019年度灘中入試問題(1日目)
大問4
A=377×377×377×377×377×377×377
とする時、Aの約数の中で14で割ると1余るものは1を含めて
全部で( ① )個あります。
また、Aの約数の中で15で割ると1余るものは1を含めて
全部で( ② )個あります。
解説
これは問題を見た瞬間に
素因数分解の問題だと気づかなければいけません。
中学受験のみならず、東大レベルでの大学受験においても
素因数分解の概念は用いられ、
特に整数問題の完答までの道のりを最短化する強力なツールなので
ぜひマスターしたい解き方ですね。
しかし、素因数分解は日常生活で出てくるシーンはあまりないので
使用するメリットがわからない、
整数問題ならではの他分野との関連性があまりない独特な解き方、
最悪、列挙のゴリ押しスタイルで解けてしまうことがある
といった理由から素因数分解が敬遠される傾向があります。
ですから、素因数分解がどういう概念であって
これを使うとどのようなメリットがあるのかを
生徒さんにプレゼンする必要があります。

では初めに素因数分解とは何かについて説明しましょう。
【素因数分解とそのメリットについて】
素因数分解とは:1を除いたすべての正の整数は素数の掛け算で表すことができる。
★つまり全ての正の整数は素数の部品で成り立っている。
※素数:2以上の自然数(1は例外)のうち、約数を2つしか持たないもの。
基本パーツとなる数と考えてください。
つまり素因数分解をすることで
その整数がどういう基本パーツからなっているか
を調べることができる
というのが大きな強みです。
例えば、24という整数を素因数分解すると、
24
=8×3
=2×2×2×3
=2の三乗 × 3
と表すことができ、
つまり
24が2のパーツが3つと、3のパーツ1つから出来ている
ということがわかります。
この最小パーツにバラして考えることで、
★★素因数分解を使うメリット★★
①約数がいくつあるかを出すことができる
②約数の総和を瞬時に出すことができる
③約数を漏れなくダブりなく列挙することができる
④元の整数が少なくとも2と3のパーツ以外からは
成り立っていないことがわかる
⑤複数の整数を素因数分解し、比較することで
最大公約数と最小公倍数が一目瞭然でわかる
という様々なメリットがあります。(その他にも多数あります。)
つまり
整数問題を見た瞬間に素因数分解をしておけば
基本的にはokということですね。
しかし、これだけ強力なツールゆえに
意味もわからず思考停止状態でとりあえず素因数分解をしている小学生が多い
という印象なので、
素因数分解の意味を理解してこのように使えば
最速で答えに向かうことができるのにな
と思うことが多々あります。
それでは本題に戻って問題にチャレンジしてみましょう。
【問題を解いてみよう】
2019年度灘中入試問題(1日目)
大問4
A=377×377×377×377×377×377×377
とする時、Aの約数の中で14で割ると1余るものは1を含めて
全部で( ① )個あります。
また、Aの約数の中で15で割ると1余るものは1を含めて
全部で( ② )個あります。
一目でわかりますが、Aは377の6乗ですよね。
まずはAがどのパーツから構成されているかを知りたいので
377を素因数分解します。
↑ (377を素因数分解すればその6乗をすればAも自明に導き出せるので
手順を効率的に簡略化することができます。)
377=13×29
です。
13も29も素数なので無事に素因数分解が完了しました。
比較的数値の大きな素数同士の組み合わせですが、
その約数を見つけるのは気合とセンスですので頑張りましょう。
377=13×29
で、Aは377の6乗ですから、
A=13の6乗 × 29の6乗
となります。
つまり
Aは13のパーツ6つと、29のパーツ6つから成り立っている
ということがわかりました。
逆に言うと、
13と29以外のパーツからは一切出来てないということもミソとなります。
つまりAの約数を列挙すると
1(13の0乗) × 29の0乗〜6乗
13の1乗 × 29の0乗〜6乗
13の2乗 × 29の0乗〜6乗
13の3乗 × 29の0乗〜6乗
13の4乗 × 29の0乗〜6乗
13の5乗 × 29の0乗〜6乗
13の6乗 × 29の0乗〜6乗
となります。
※自然数の0乗は必ず1です。
(つまり7×7の49個約数があります)
一見難しいことを書いているように見えますが、
13と29の約数の組み合わせを互いに6つという制約のもと
漏れなくダブりなく列挙しているだけです。
ここで( ① )に取り掛かりましょう。
今回は約数を14で割ったときの余りに注目する問題でしたよね。
ですから
それぞれのパーツを掛け算する前に
予め14で割っておけばいいわけです。←これめちゃくちゃ大事
(この概念は大学受験ではmodと表し、バリバリ大学受験でも大活躍します。)
わざわざ掛け算した後の馬鹿でかい数を手間暇かけて割り算して
余りを出すよりも前もって数が小さい段階で下準備した方が楽だよねという
発想です。
この時、29は14で割ると1余ります。
つまり、
29は何乗しようが絶対に1余ることになります。
(1×1×1×1×1×1×1×……=1となるから。当たり前だけど。)
13は
0乗の時は1余り、
1乗の時は13余り
2乗の時は13×13=169ですから、14で割ると12余る1となり1余る
3乗の時は169×13ですから余りだけに注目すると1×13=13となり13余る
同様にしてそれぞれの約数を14で割った時の
図を上の図に照らして書くと
14で割った時の余り
1(13の0乗) × 29の0乗〜6乗
➡︎1×1=1 ゆえに1余る!!
13の1乗 × 29の0乗〜6乗
➡︎13×1=13 ゆえに13余る
13の2乗 × 29の0乗〜6乗
➡︎1×1=1 ゆえに1余る!!
13の3乗 × 29の0乗〜6乗
➡︎13×1=13 ゆえに13余る
13の4乗 × 29の0乗〜6乗
➡︎1×1=1 ゆえに1余る!!
13の5乗 × 29の0乗〜6乗
➡︎13×1=13 ゆえに13余る
13の6乗 × 29の0乗〜6乗
➡︎1×1=1 ゆえに1余る!!
1余るカタマリは4ブロックあり、
一つのカタマリあたりに0乗~6乗の7つの数字がありますから、
ゆえに( ① )の答えは
7×4=28個
となりますね。
次に( ② )について考えてみましょう。

約数のうち、15で割って1余るものが何個あるかという話ですよね。
先程と異なり、
どちらかは何乗しても1余るというものがないのが面倒なポイントです。
ですから13と19のそれぞれ0乗から6乗までの余りを書き出す必要があります。
しかし、2乗ぐらいならまだしも、
いちいち律儀に5乗して割り算して余りを出したりしていたら
計算が煩雑すぎて時間が絶対に足りなくなります。
ですからここで時短テクニックを使う必要があります。
★時短テク
余りだけを出したい時は
元の余りだけを掛けて割るだけでOK
ある整数Xの0〜a乗までのそれぞれの乗数をある整数Yで割った時の余りは、
前の乗数をYで割った時の余りにXをかけて、それをYでもう一度割れば良い。
というものです。
何を言っているかおそらく何を言っているか意味不明な呪文のように見えると思うので
とりあえず実演してみましょう。
13の0〜6乗を15で割った時の余りについて考えてみましょう。
0乗:1なので自明に1余る。
1乗:13なので自明に13余る。
2乗:13×13=169 となり、15で割ると11余る4となる。
3乗:ここからが時短テクニックが使えます。
わざわざ13×13×13をして15で割る必要がありません。
2乗の時の余りである4に13をかけて15で割れば余りが簡単に出せます。
つまり、4×13=52となり、15で割ると7余ることがわかります。
また、これは余りに元の数を掛けるだけでなく、
元の数をすでに15で割った時の余りを掛けることでさらに時短することも可能です。
(つまり、29の乗数の場合、余りに29をかけるのではなく、
予め15で割った時の余りである14を掛けてOKです。)
※この時短テクニックの証明は最後に載せておきますね。
同様にして13と29の0〜6乗をそれぞれ15で割った時の余りを
図示すると以下の通りになります。
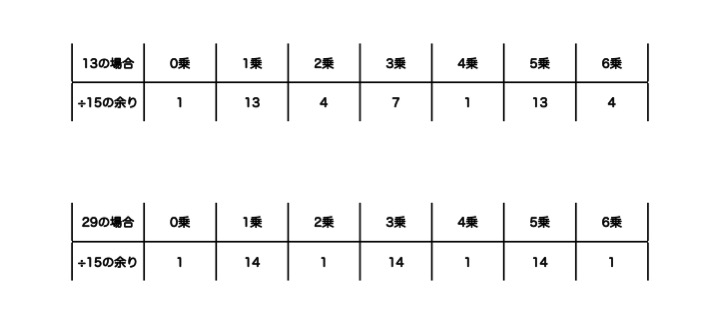
約数のうち、15で割った時の余りが1ということは
つまり1は整数の掛け算で表すと
1=1×1しかありえませんから、
(15で割った時) 余りが1となる13の乗数 × 余りが1となる29の乗数
に絞られることがわかります。
つまり、上の図を見ればわかる通り、
(13の0,4乗) × (29の0,2,4,6乗)
に組み合わせが絞られます。
ですから( ② )の答え、つまりAの約数のうち、15で割って1余る数は
2×4=8個
あることが導き出せました。
【まとめ】
灘中の問題はいかがだったでしょうか。
文字で丁寧に説明するとものすごくボリューミィな内容になってしまいましたが、
構造はいたってシンプルな解いてて楽しい問題です。
頭を使えばこのように煩雑な計算を極力減らすことができますからね。
生徒さんも最初はちんぷんかんぷんでしたが、一緒に解いてみると
「あーそういうことか!!!簡単じゃん!!!」となっていました。
この時期に変にハードルを上げすぎない、意外と解けるんだ
という感覚を持たせることが大事だと考えています。
普段のテストに追われている時期にこのような遊びはなかなかできませんが、
テスト終わりにコーヒーブレイク感覚でこのような遊びをするのも
いいなと感じました。
とはいえ、筑駒と並んで日本最難関の中学である灘の問題は一味違いますね。
普通に大学受験でも通用するmodの問題をサラッと中学受験で聞きますからね。。
さすが、学年の半分が東大に進学するスーパーエリート校は格が違うな…
と感じた問題でありました。
それでは今日はこの辺りで失礼させていただきます。
次回の記事でお会いしましょう。さようなら。
毎度たくさんの人に読んでいただきありがとうございます。
先日ブログ村の会員になりました。もしこの記事が少しでもいいなと感じていただけたら是非このボタンをクリックしていただきたいです!!管理人がものすごく喜びます!!
【補足(時短テクの証明)】
